To find the volume of the rectangular prism, we multiply the length by the breadth. To find the area of the two dimensional figure at the base and then measure the 3D solid by multiplying again by the height. Length times width times height would give you the volume of any rectangular prism. And once you enter the third dimension your measurements have to be in cubic units like these cubic centimeters. And once you enter the third dimension your measurements have to be in cubic units like these cubic ... This lesson uses a discovery approach to exploring the meaning of volume.
In this lesson students will extend their knowledge of volume from using whole numbers to using fractional units. In geometry classes, students are often assigned worksheets in which they must calculate the volume, cross-section, or surface area of a rectangular prism. At first glance, this might seem tricky, but it really comes down to a simple formula. In this guide, we'll explain the concept of rectangular prisms, break down the volume formula, and give real examples. Look at the right rectangular prisms below. Fill the prisms with unit cubes of the appropriate unit fraction edge lengths.
Ask students if they think this formula will work for right prisms with bases that are not triangles. Have them reconstruct their right rectangular prisms, reviewing the formula. Have students measure the area of their bases and then multiply this amount by the height of their prisms.
Their total should be close to 100, depending on how accurate their measurement and method of multiplication. Now ask students, "How can we use the number of cubic centimeters in each layer and the number of layers in the prism to compute the volume? " Students may suggest addition or multiplication. For example, students may suggest adding 48 + 48 + 48 for Prism F because there are 3 layers. Remind students that multiplying 48 and 3 does the repeated addition suggested here. Ask students to use the information in this table to compute the volume of each prism F, G, H, and I.
The volume of a rectangular prism formula is obtained by multiplying the length, breadth and height of the prism. To recall, a prism that has 2 parallel rectangular bases and 4 rectangular faces is a rectangular prism. The mathematical literature suggests to any polyhedron like this as a Cuboid.
It has 6 flat rectangular faces and all the angles are right-angled. The other names of such rectangular prism are rectangular hexahedron, rectangular parallelepiped and right rectangular prism. Finding the Volume of Solid Figures MCC6.G.2 – Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes. For this activity, students will develop the formula for finding the volume of a rectangular prism. Each group of students will receive a container of unit cubes . Each student will have five minutes to create their own rectangular prism.
After five minutes students will be directed to count the cubes to find the length, width and height of their polyhedron. I will then ask them to deconstruct their polyhedron and count how many cubes they used in total to construct it. I will explain to students that the total count of cubes is the volume of the rectangular prism and I will give them a formal definition of volume. Give each student, or pair of students, one 5 oz.
Can of Play Doh equal to 100 cm3 and a plastic knife. Review exactly what a right rectangular prism is, recognizing that there are many possible dimensions that can fit the definition. Each prism must have two rectangular bases and sides that join at right angles. Discover that the side faces are also rectangles. Discover that there are 6 total faces, all rectangles. Discuss that the bases or side faces or both may also be squares, since squares are special rectangles.
Review the vocabulary of solid figures so students are conversant with these terms. Prisms in items must be right rectangular prisms. Unit fractional edge lengths for the unit cubes used for packing must have a numerator of 1. Many shapes in our world, such as cereal boxes and bricks, are rectangular prisms.
Often, we have to know how much volume a rectangular prism takes up. In this lesson, learn how to calculate the volume of a rectangular prism. This two-day lesson uses a hands-on problem solving approach to find the volume of a right rectangular prism with fractional edges. Students first design boxes and fill with Rubik's Cubes. They create a formula from the patterns they found.
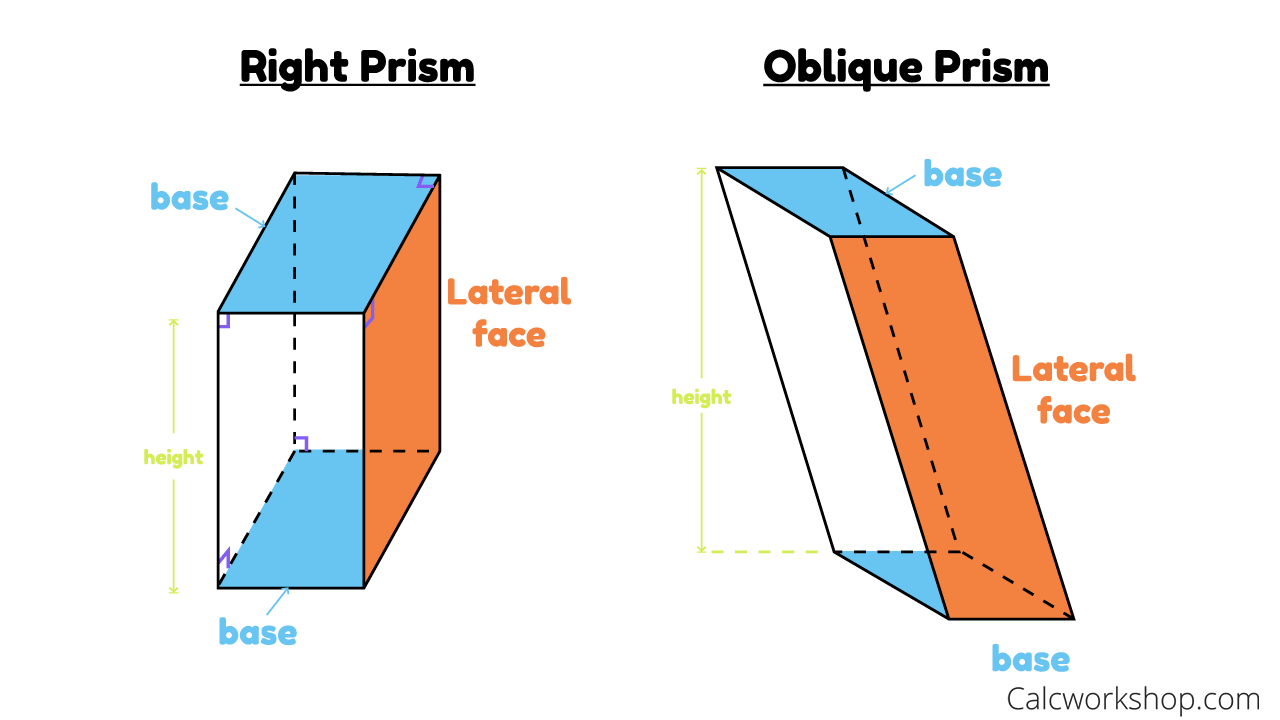
Using cubes with fractional edges requires students to apply fractional units to their formula. Compute the volumes of rectangular prisms using the volume formulas. Prisms are of different types named as triangular prisms, square prisms, rectangular prisms, pentagonal prisms, hexagonal prisms etc. They are the right rectangular prism and oblique rectangular prism.
In this article, we will discuss rectangular prisms, their properties, formulas to calculate the area and volume of a prism. Volume word problems require making calculations of volumes of three-dimensional shapes using volume formulas. To calculate the volume, plug the given dimension into the relevant volume formula. Make finding the volume of a rectangular prism a snap by using a formula! If you already know the length, width, and height.
In this tutorial, you'll see how to use that information and the formula for the volume of a rectangular prism to get the answer. Solve real-world and mathematical problems involving area, volume and surface area ... A right prism is in the shape of a geometric solid that has a polygon as its base and vertical sides perpendicular to the base.
The base and top surface are of the same shape and size. It is called a "right" prism because the angles between the base and sides are right angles. Examples of right prisms are a rectangular prism, a cube, a triangular prism and a cylinder. A flat shaped like, a rectangle has two dimensions, length and width.
But a solid like this rectangular prism is 3D. The height is what we were measuring when we counted the layers upwards and again because we built the shape from centimeter cubes. We know that each cube side measures one centimeter. So the height of the solid is two centimeters. A prism is a solid figure that has two parallel congruent sides that are called bases that are connected by the lateral faces that are parallelograms. There are both rectangular and triangular prisms.
In geometry, a rectangular prism is a polyhedron with two congruent and parallel bases. It is called prism because it forms a cross-section along the length. In this section, we will discuss the definition of a rectangular prism, types, volume formula, and the volume of a rectangular prism.
A prism is a 3-dimensional shape with two identical shapes facing each other. These identical shapes are called "bases". The bases can be a triangle, square, rectangle or any other polygon.
Other faces of a prism are parallelograms or rectangles. The volume of a triangular prism can be found by multiplying the base times the height. Both of the pictures of the Triangular prisms below illustrate the same formula. The formula, in general, is the area of the base times the height, h. In this lesson, students extend this idea to prisms with fractional side lengths. They build prisms using unit-fraction cubes.
The volume is the number of unit-fraction cubes in the prism times the volume of each unit-fraction cube. Students show that this result is the same as the volume found by using the formula. Many students will calculate that the product of the length, width, and height will give them the volume of the polyhedron.
I will encourage them to test their theory on each of the groups' polyhedron. When students have confirmed that the relationship is true for all rectangular prisms, I will give them the formula for volume of a rectangular prism. This lesson introduces the idea of finding volume. Students will be left to design their own data collection and organizing the data that they collect. They will apply the skill of finding volume to using fractional parts of a number and finding the product using the volume formula. Observe whether or not students are filling the prism with cubic-centimeter blocks to verify their volume computations.
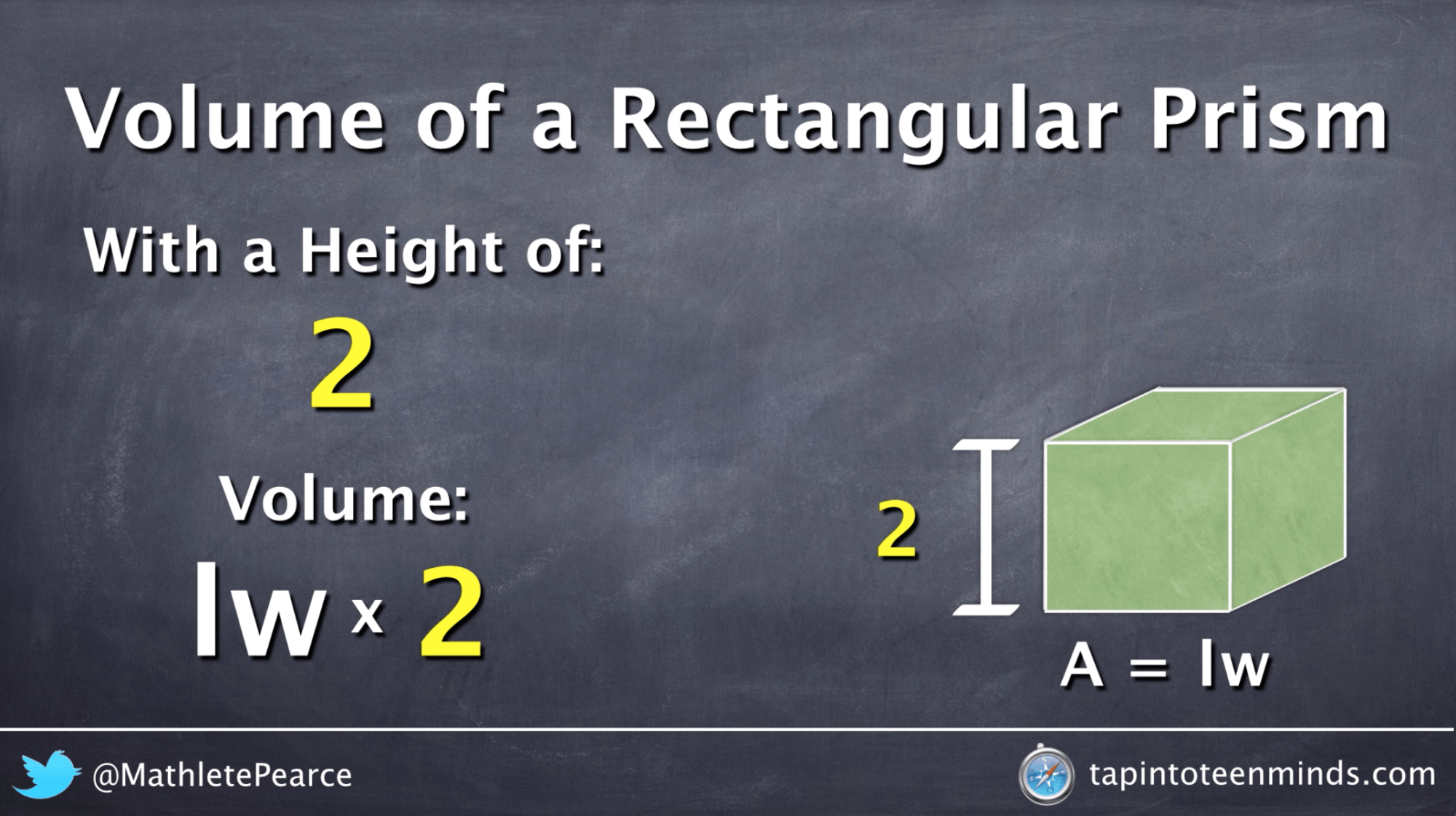
Prism F requires 144 cubic centimeters to fill the prism. This was done intentionally so students may choose to start thinking of more efficient ways to determine how many blocks will be needed to fill the prism. Some groups may recognize that they need only form the bottom layer of blocks and then determine how many layers there would be. This formula computes the volume of the prism by multiplying the number of blocks in one layer by the number of layers of blocks are needed to fill the prism .
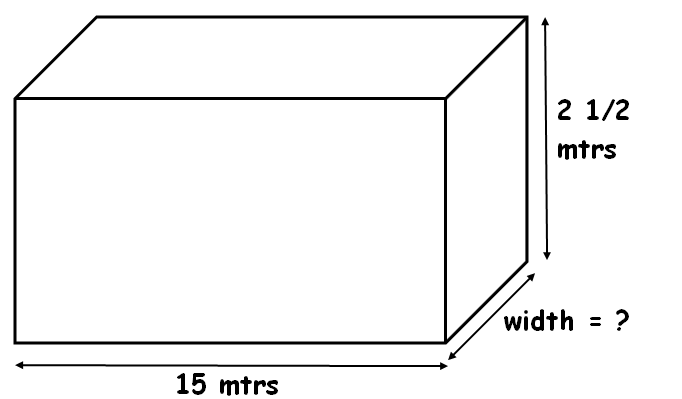
In a rectangular prism the bases or ends are rectangular faces and the lateral faces or side faces are also rectangles. Formula for the volume of a rectangular prism. The volume of a rectangular prism of length l, width w and height h is given by the formula.
The product of the length and width of the base of the rectangular prism gives the ... Like all three-dimensional shapes, a rectangular prism also has volume and surface area. The volume of a rectangular prism is a measurement of how much volume is occupied by a rectangular prism.
The volume of a rectangular prism is denoted by cubic units. It can also be defined as the number of units used to fill a rectangular prism. The following table gives the volume formulas for solid shapes or three-dimensional shapes.
Scroll down the page if you need more explanations about the volume formulas, examples on how to use the formulas and worksheets. The volume of a rectangular prism is the measure of the space the fills it. In this article, you will learn how to find a rectangular prism volume by using the volume of a rectangular prism formula. We will also discuss the volume of a spherical cylinder.
The measurement of the length is 2½ inches. The measurement of the width is 3 ½ inch. The measurement of the height is 4 inches.
How many cubes with side lengths of 1/2 inch would be needed to fill the prism? The measurement of the length is 3/4 inches. The measurement of the height is 2 inches. How many cubes with side lengths of 1/4 inch would be needed to fill the prism? The measurement of the length is 4 1/2 inches.
The measurement of the width is 1 ½ inch. The measurement of the length is 1½ inches. Students are asked to determine the volume of a right rectangular prism given fractional edge lengths. It will be difficult for students to understand why this second formula is needed, as the first formula seems sufficient. However, this second formula is very important as it can be used to find the volume of all right prisms and cylinders too. Surface Area of a Rectangular Prism Formula.
The surface area of a Rectangular Prism would be the sum of the area of lateral faces and its rectangular bases. The surface area is usually measured in square units. Where, b – base length of the rectangular prism.
L – base width of the rectangular prism. The surface area of a rectangular prism is the measure of how much exposed area a prism covers. The surface area of a rectangular prism is the sum of the lateral surface area along with twice the base area of the rectangular prism.














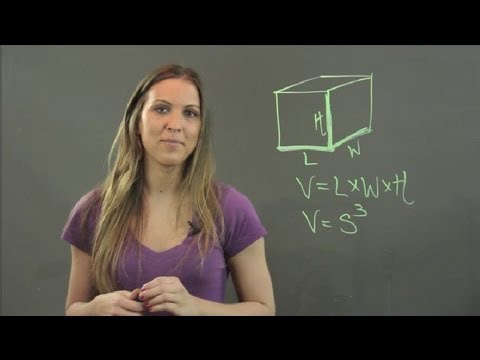







No comments:
Post a Comment
Note: Only a member of this blog may post a comment.